Determine The value of limit f(x) for x approuch to c Padahal 0 <> Masing-masing ruas kalikan dengan Dan Bukti: Dan Apabila menemui bentuk Adapun rumus-rumus trigonometri yang dapat digunakan adalah sebagai berikut:
Menentukan Nilai limit f(x) untuk x mendekati c
1. Subtitute c f (x) so the value is f (c)
Subtitusikan c pada f (x) sehingga nilainya adalah f (c)
2. apabila didapat bentuk tak tentu , maka ubahlah bentuknya sehingga diperoleh bentuk tentu. Yaitu dengan mengalikan dengan bentuk sekawannya, menfaktorkan, membagi dengan variabel berpangkat tertinggi (pada limit ![]() ), merubah nama (pada limit fungsi trigonometri), dll.
), merubah nama (pada limit fungsi trigonometri), dll.
Teorema-teorema limit:
1. Jika c dan k adalah kontanta maka 
2. Jika c dan k adalah kontanta dan f adalah suatu fungsi x, maka 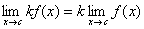
3. Jika c adalah konstanta dan f adalah suatu fungsi x, maka  .
.
4. Jika c adalah konstanta dan f dan g adalah fungsi-fungsi dari x, maka  .
.
5. Jika c adalah konstanta dan f dan g adalah fungsi-fungsi dari x, maka  .
.
6. Jika c adalah konstanta dan f dan g adalah fungsi-fungsi dari x, maka
7. Jika c adalah konstanta dan f fungsi dari x, maka  .
.
Limit Fungsi Aljabar Berbentuk 
Jika diketahui 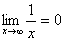 .
.
1. Untuk fungsi rasional
maka nilai limitnya adalah
· Jika m = n, maka  .
.
Bukti:
apabila di subtitusikan langsung maka akan diperoleh bentuk tak tentu  , sehingga
, sehingga  harus diubah sedemikian hingga apabila disubtitusikan menjadi bentuk tentu, dan diketahui bahwa:
harus diubah sedemikian hingga apabila disubtitusikan menjadi bentuk tentu, dan diketahui bahwa: dengan n adalah sembarang bilangan rasional. Yaitu dengan cara membaginya dengan x berpangkat tertinggi.
dengan n adalah sembarang bilangan rasional. Yaitu dengan cara membaginya dengan x berpangkat tertinggi.
· Jika  dan
dan  , maka
, maka 

apabila di subtitusikan langsung maka akan diperoleh bentuk tak tentu , sehingga  harus diubah sedemikian hingga apabila disubtitusikan mejadi bentuk tentu, dan diketahui bahwa
harus diubah sedemikian hingga apabila disubtitusikan mejadi bentuk tentu, dan diketahui bahwa , dengan n adalah sembarang bilangan rasional. Yaitu dengan cara membaginya dengan x berpangkat tertinggi. Dalam hal ini pangkat tertingginya adalah n, karena
, dengan n adalah sembarang bilangan rasional. Yaitu dengan cara membaginya dengan x berpangkat tertinggi. Dalam hal ini pangkat tertingginya adalah n, karena 

· Jika  , maka
, maka  . Identik dengan bukti sebelumnya hanya saja karena maka misal s > 0 dengan
. Identik dengan bukti sebelumnya hanya saja karena maka misal s > 0 dengan  , maka nilai limitnya dapat ditulis sebagai
, maka nilai limitnya dapat ditulis sebagai .
.
· Jika  , maka
, maka . Untuk bukti yang ini ditinggalkan sebagai latihan.
. Untuk bukti yang ini ditinggalkan sebagai latihan.
Apabila anda telah mengetahui hal ini maka anda dapat memanfaatkannya dalam menghadapi ujian yaitu dengan mengidentifikasi pangkat tertinggi dari variabel pada pembilang dan penyebutnya.
2. Untuk  .
.
· Jika  , maka
, maka  .
.
Bukti:
Karena  maka
maka , sehingga variabel berpangkat tertingginya adalah
, sehingga variabel berpangkat tertingginya adalah  , sehingga diperoleh:
, sehingga diperoleh:
· Jika  , maka
, maka  .
.
Apabila anda telah mengetahui hal ini maka anda dapat memanfaatkannya dalam menghadapi ujian yaitu dengan memperhatikan koefisien variabel –variabel berpangkat tertinggi.
Limit Fungsi Trigonometri
A.  dan
dan 
Bukti:
Perhatikan gambar berikut
Misalkan α adalah sudut lancip pada juring lingkaran dengan jari-jari 1 satuan. Titik  , B (1, 0) dan
, B (1, 0) dan  . Dari gambar tersebut diperoleh:
. Dari gambar tersebut diperoleh:
i) Luas segitiga OBP = 
ii) Luas juring OBP = 
iii) Luas segitiga OBQ =

 , maka subtitusikan langsung, apabila menghasilkan bentuk tak tentu, maka ubahlah dalam sin
, maka subtitusikan langsung, apabila menghasilkan bentuk tak tentu, maka ubahlah dalam sin

Bentuk-bentuk yang terdapat dalam limit fungsi trigonometri, yang biasanya rumit pengerjaannya:
Learning with Me
This site provides information needed by students.
Adds by Google
Labels
- English (15)
- Lain-lain (6)
- Mathematics (8)
Blog Archive
Followers
Playlist
Guest Book
Calendar
Word of the Day
Free content
provided by The Free Dictionary
Article of the Day
Free content
provided by The Free Dictionary
This Day in History
Free content
provided by The Free Dictionary
Today's Birthday
Free content
provided by The Free Dictionary
In the News
Free content
provided by The Free Dictionary
Quotation of the Day
|
Life does not cease to be funny when people die any more than it ceases to be serious when people laugh.
George Bernard Shaw (1856-1950) |
Free content
provided by The Free Library
Match Up
Free content
provided by The Free Dictionary
Hangman
Free content
provided by The Free Dictionary
Blogroll
- MTsN Lawang
- Adsense Information
- Blogger Templates
- Info Beasisswa
- Video
- Anak Laut
- Internet Marketing and Trading
- Geologi
- In the line of life
- Lagu top masa kini
- Edit tag
- Games
- Koleksi lirik Lagu
- Nizam Zakaria
- teknoblogia
- Info kerja
- Camera Toss
- Info Teknologi
- Berita Lingkungan
- Mungil
- Ebookmania
- The History of Indian Muslim
- Informatika Kesehatan Masyarakat & Kedokteran
- Info Komputer
Copyright 2009
Learning with Me
Web Design
:Ray Creations. Sponsored by
Web Hosting India and
Ray Hosting.











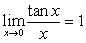



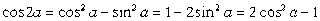


















1 comments:
kog besar2, jadi bingung bacanya... hehe
Post a Comment