Practice

Jarak Titik ke Titik

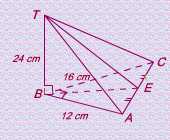
Dari limas T. ABCD diketahui bahawa segitiga ABC siku-siku di
titik B. AB = 12 cm, BC = 16 cm,
TB = 24 cm, dan garis TB tegak lurus bidang ABC.
Hitunglah jarak antara titik T dan titik tengah AC.

Solusi :

Perhatikan gambar.


AC ² = √ AB ² + BC ²

= √ 12 ² + 16 ²
= 20 cm

Luas ΔABC =½ AB x BC

= ½ x 12 x 16 = 96 cm ²

BE ² = ½ AB ² + ½BC ² - ¼ AC ²
= ½ ( AB ²+ BC ²) - ¼ AC²
= ½ AC ²- ¼ AC ²
= ¼ AC ² BE = ½ AC
= ½ x 20 = 10 cm

TE = √ TB ² + BE ² = √ 24 ² + 10 ²= √ 676 = 26 cm

Jadi jarak antara titik T dan titik tengah AC adalah 26 cm.

Diketahui kubus ABCD. EFGH, dengan panjang rusuk 6 cm. Titik
P, Q, dan R berturut-turut terletak pada pertengahan garis
AB, BC, dan bidang ADHE.

Tentukan jarak dari titik P ke titk R dan jarak dari titik Q
ke titik R.

Solusi :

Perhatikan gambar

ΔPAR siku-siku di titik A, dengan AP = ½ AB = 3 cm

dan AR = ½ √ AD ² + DH ² = ½ √ 6 ²+ 6 ² = 3√ 2 cm

sehingga:

PR = √ AP ² + AR ² = √ 3 ² + (3√ 2)² = √ 27 = 3 √ 3 cm

Jadi jarak titik P ke titik R adalah 3 √ 3
cm.

Perhatikan gambar.

Δ QRS siku-siku di titik S, dengan QS = 6 cm

dan RS = ½ AE = cm , sehingga:

QR = √ QS ² + R ² = √ 6 ² + 3 ²= √ 45= 3 √ 5 cm

Jadi jarak titik Q ke titik R adalah 3 √ 5 cm.