space figures

Dimensi Tiga

Pembagian Bangun Ruang
Bangun ruang dibagi menjadi:
1. Bangun ruang sisi datar
2. Bangun ruang sisi lengkung
Bangun ruang sisi datar meliputi:
1. Prisma
2. Balok
3. Kubus
4. Limas
Bangun ruang sisi lengkung meliputi:
1. Tabung
2. Kerucut
3. Bola


1. Prisma
Prisma adalah Bangun ruang yang mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran.

Contoh:

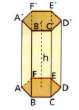
Prisma segilima, penampang melintangnya berbentuk segi lima beraturan.
Volume Prisma
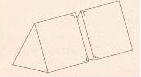
Misalkan kita memiliki benda seperti pada gambar dibawah. Potongan tegak lurus terhadap suatu rusuk dan sejajar dengan salah satu sisi akan menghasilkan bentuk yang sama. Dalam hal ini hasil potongan berbentuk segitiga.


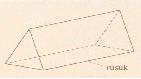
Hasil potongan ini dapat dilihat pada gambar berikut.

Benda-benda seperti di atas disebut sebagai PRISMA TEGAK

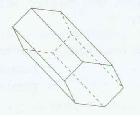
Gambar Potongan berbentuk Segienam di atas juga memiliki sifat yang sama dengan prisma
Balok juga dapat dipandang sebagai prisma dengan potongan berbentuk persegi panjang. Volume balok adalah
V = panjang x lebar x tinggi
= panjang x ( lebar x tinggi )
= panjang x luas potongan
dengan luas potongan adalah luas daerah yang diarsir.
Sekarang, jika kita memiliki prisma dengan potongan berbentuk segitiga
kita dapat melihatnya sebagai bagian dari balok.
Sehingga volumenya adalah
Volume prisma segitiga = panjang x (1/2 x lebar x tinggi)
= panjang x luas segitiga
= panjang x luas potongan

2. Balok
Balok adalah Bangun ruang yang dibatasi oleh enam persegi panjang yang pasangan-pasangan sisinya saling sejajar atau prisma yang penampang melintangnya berupa persegi panjang.
contoh benda yang termasuk balok:

Volume Balok
Volume sebuah kubus yang berukuran 1cm, akan disebut sebagai volume benda sebesar 1 cm³.
Volume sebuah bangun ruang adalah perbandingan volume benda dengan volume kubus 1 cm³.
Selain ukuran cm, dapat pula digunakan ukuran panjang yang lain.

Misalkan kotak berukuran 8 cm, 4cm. dan 2 cm maka dapat disusun suatu kubus yang berukuran 1 cm3 sepanjang 4 lajur dan akan berisi 8 buah sebanyak 2 lapis.
Jadi banyak kubus satuan yang dapat dimuat oleh kotak tersebut adalah 8 x 4 x 2
Bilangan inilah yang disebut volume kotak dan ditulis sebagai V= 64 cm3

jadi volume Balok adalah:
Volume = p x l x t
Luas Permukaan Balok
Balok memiliki permukaan yang terdiri dari 6 persegi panjang.
Luas persegi panjang tersebut adalah

Luas _ABCD =Luas_EFGH = p x l
Luas _BCGF =Luas_ADHE = l x t
Luas _ABFE =Luas_DCGH = p x t

Dengan demikian luas permukaan balok adalah jumlah ketiganya dikali 2, yaitu
Luas permukaan balok = 2 x ( p x l + l x t + p x t)
dengan p, l, dan t adalah ukuran balok

3. Kubus
Kubus adalah bangun ruang yang dibatasi oleh enam persegi yang berukuran sama atau balok yang semua sisinya sama.

contoh benda yang termasuk kubus:

Volume dan Luas permukaan Kubus
Berdasarkan definisinya, misalkan rusuknya = r, maka volume kubus adalah:
volume = r x r x r = r³
Dan luas permukaan kubus adalah:
luas permukaan kubus = 6 x r x r = 6r²

4. Limas
Limas adalah bangun ruang yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. Limas adalah benda yang alasnya berbentuk segi n dan sisinya terdiri atas n segitiga.

contoh benda yang termasuk limas :

Piramida di Mesir merupakan contoh limas segiempat karena alas dari piramida adalah segiempat. Untuk menghitung volum limas, perhatikan kubus ABCD.EFGH dengan panjang rusuk a cm.
Dengan menarik diagonal AF, FC, FD, dan FH, maka terdapat tiga limas segiempat yaitu F.ABCD, F.ADHE, F.CGHD. Ketiga limas tersebut mamounyai bentuk yanng sama. Jadi
Volume _F.ABCD = Volume_F.ADHE = Volume_F.CGHD Karena
Volume_F.ABCD + Volume_F.ADHE + _VolumeF.CGHD = Volume Kubus

makaVolume_F.ABCD = 1/3 x Volume Kubus= 1/3 x Luas_ABCD
= 1/3 x Luas alas x tinggi

Lingkaran dapat dipandang sebagai segi-n dengan n sangat besar
Kerucut adalah limas dengan alas berbentuk lingkaran, dapat dipandang sebagai limas segi n dengan n sangat besar. Garis l pada kerucut disebut garis pelukis.

5. Tabung
Tabung adalah limas yang penampang melintangnya berbentuk lingkaran.

contoh benda yang termasuk tabung:

Luas permukaan prisma dan tabung
luas permukaan prisma secara umum adalah:luas permukaan = keliling alas x tinggi

6. Kerucut
Kerucut adalah limas yang alasnya berbentuk lingkaran.

7. Bola
Bola adalah tempat kedudukan titik-titik dalam benda ruangyang berjarak tetap terhadap suatu titik tertentu.
contoh benda yang termasuk bola:

Volume Bola
Untuk menghitung volume bola, kita perlu menggunakan prinsip Cavalieri. Dua buah benda yang mempunyai tinggi dan luas potongan yang sama. Perhatikan Gambar berikut


Demikian pula silinder tegak dan silinder miring ini akan mempunyai volume yang sama.


Sekarang, kita misalkan kita mempunyai silinder atau tabung berjari - jari r cm dan tinggi 2r cm. Pada silinder ini diambil dua kerucut yang berjari - jari r cm dan tinggi r cm.


Tampak depan kedua benda bila dipotong oleh bidang tegak terhadap silinder sejauh a dari pusat bola atau puncak kerucut adalah


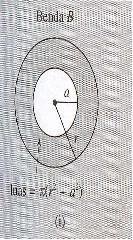
Akibat perpotongan bidang tersebut, tampak atas perpotongan dari masing - masing benda adalah seperti ditunjukkan pada gambar berikut



Mudah dibuktikan bahwa kedua potongan ini sama luasnya. Karena kedua benda memiliki tinggi yang sama, maka keduanya mempunyai volume yang sama. Volume itu adalah

Volume Bola = Volume benda B
= Volume tabung - 2 x Volume kerucut
= 22/7r² - 2 x 1/3 x 22/7r² x r
= 4/3 22/7r³

Jadi, volume bola adalah

Volume Bola = 4/3 22/7r³